
Now, enter the values appropriately and accordingly for the parameters as required by the example above where the base area of the prism is 30 cm 2 and the height of the prism is 8 cm.Īs you can see from the screenshot above, Nickzom Calculator – The Calculator Encyclopedia solves for the volume of a prism and presents the formula, workings and steps too. This function calculates the height or volume of a regular hexagonal prism. The screenshot below displays the page or activity to enter your values, to get the answer for the volume of a prism according to the respective parameters which are the base area and height of the prism. The general formula to find the volume of any prism is: Volume (V) Base Area × Height, here, the height of any prism is the distance between the two bases. Now, click on Volume of a Prism under Mensuration i.e., volume of a prism base area × height of the prism.

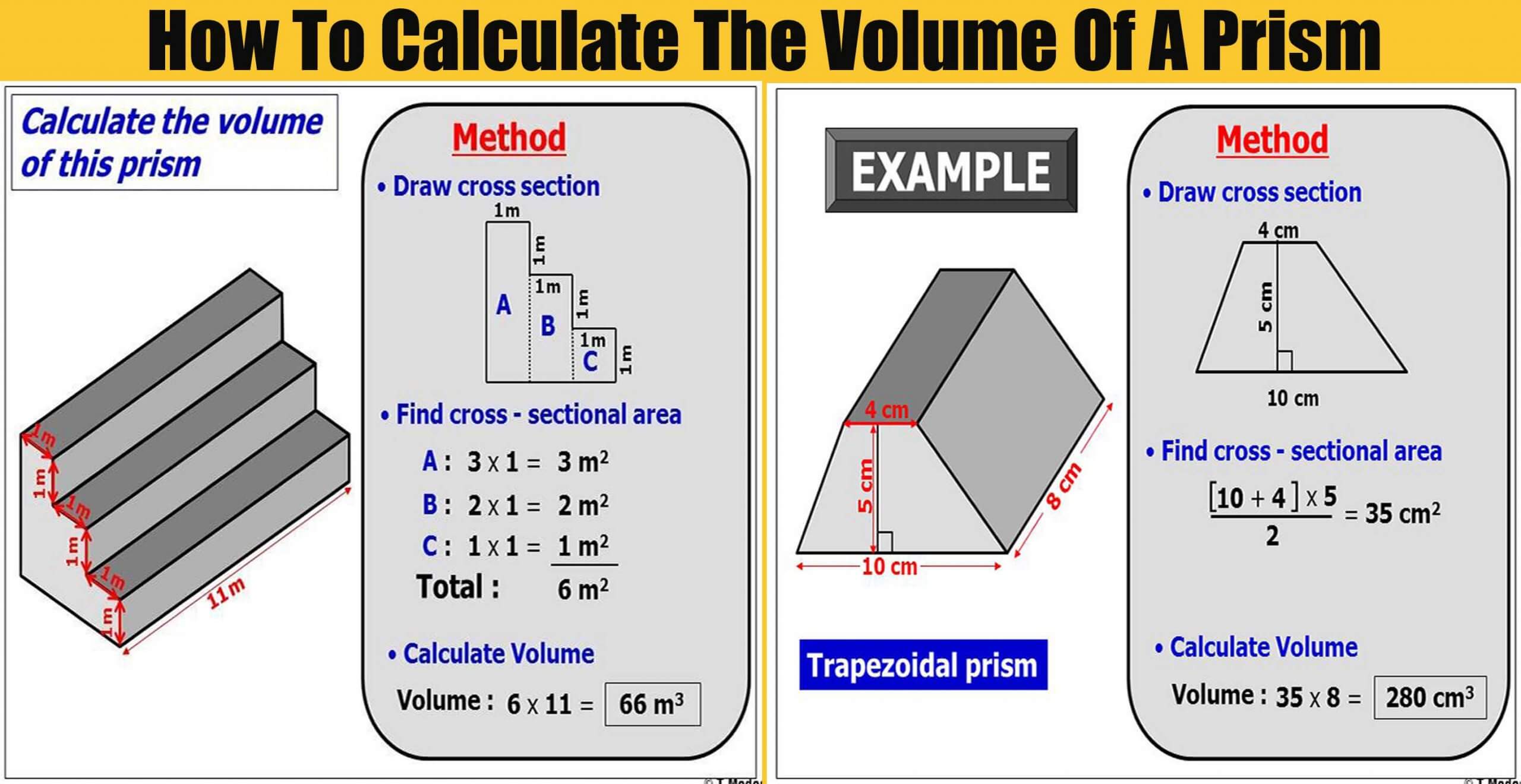
Once, you have obtained the calculator encyclopedia app, proceed to the Calculator Map, then click on Mensuration under the Mathematics section. The volume of a prism can be obtained by multiplying its base area by total height of the prism. recognise a prism use the formula for the volume of a prism find the. To get access to the professional version via web, you need to register and subscribe for NGN 1,500 per annum to have utter access to all functionalities. calculate lengths, areas and volumes in plane shapes and right prisms. You can get this app via any of these means: To calculate the volume of a prism, we find the area of the cross section and multiply it by the depth. To get the answer and workings of the volume of a prism using the Nickzom Calculator – The Calculator Encyclopedia. First, you need to obtain the app. Nickzom Calculator – The Calculator Encyclopedia is capable of calculating the volume of a prism. Therefore, the height of the prism is 8 cm. The formula is simply V 1/2 x length x width x height. Therefore, the base area of the prism is 25 cm 2.Ĭalculating the height of a prism when Volume and Base area are Givenįind the height of a prism with a volume of 280 cm 3 and a base area of 35 cm 2 1.Write down the formula for finding the volume of a triangular prism. Therefore, the volume of the prism is 240 cm 3.Ĭalculating the Base area of a prism when Volume and Height are Givenįind the base area of a prism with a volume of 300 cm 3 and a height of 12 cm. The formula for computing the volume of a prism is:įind the volume of a prism with a base area of 30 cm 2 and a height of 8 cm. Every rectangular prism has: 8 vertices 12 sides and 6 sides. Thus, the unit of volume of the prism is given as V (square units) × (units) cubic units. Given the surface area, length and width find the height, volume and diagonal of a rectangular prism. The unit of base area is given in square units and the height of the prism is given in units. Given the length, width and height find the volume, surface area and diagonal of a rectangular prism. The volume formula for a cylinder is height x x (diameter / 2)2, where (diameter / 2) is the radius of the base (d 2 x r), so another way to write it is height x x radius2. To compute the volume of a prism requires two essential parameters which are the base area and height of the prism. Thus, the volume of a prism can be given as V B × H where V is the volume, B base area, and H height of the prism.
#Calculate volume of a prism how to#


Formula for the volume of a rectangular prism: 3. How to Convert Bytes/second to STM-64 (signal) | Data Transfer Rate Units Prism volume (V) B × h, where, B is the area of the base and h is the height of the prism.For example, if you are starting with mm and you know a and h in mm, your calculations will result with V in mm 3.īelow are the standard formulas for volume. The units are in place to give an indication of the order of the results such as ft, ft 2 or ft 3. Units: Note that units are shown for convenience but do not affect the calculations. Online calculator to calculate the volume of geometric solids including a capsule, cone, frustum, cube, cylinder, hemisphere, pyramid, rectangular prism, sphere and spherical cap.


 0 kommentar(er)
0 kommentar(er)
